Charlando con un amigo (¡todo un genio!) surgió el tema relacionado a con que las matemáticas están llenas de números que parecen tener poderes mágicos.

Estos números aparecen una y otra vez en la naturaleza, el arte, la física y la tecnología. No son solo abstracciones: son las firmas matemáticas del universo.

Por lo tanto me dí a la tarea de investigar un poco más acerca de la magia de las matemáticas.

Como todas las semanas, en Neurospicolocos, te presentamos los números más fascinantes y, sobre todo, por qué estos son tan importantes.

🌀 φ (Phi) — La proporción áurea ≈ 1.618…

¿Qué es? La proporción áurea es un número especial que aparece cuando divides una línea en dos partes de modo que la razón entre la línea completa y la parte más larga es igual a la razón entre la parte más larga y la más corta.

Matemáticamente: φ = (1 + √5) / 2 ≈ 1.618033988…

¿Por qué es fascinante? Phi está profundamente conectado con la secuencia de Fibonacci (lo veremos más adelante) y aparece constantemente en:

• Arte y arquitectura: El Partenón, las pirámides de Egipto y pinturas del Renacimiento usan esta proporción porque es estéticamente agradable al ojo humano
• Anatomía humana: La relación entre la altura total y la altura hasta el ombligo se aproxima a phi; lo mismo con las falanges de los dedos
• Galaxias espirales: La estructura de brazos espirales de galaxias sigue esta proporción
• Plantas: La disposición de las hojas alrededor del tallo (filotaxis) y la forma de muchas flores siguen patrones relacionados con phi

1, 1, 2, 3, 5, 8, 13… — Los números de Fibonacci

¿Qué son? Una secuencia donde cada número es la suma de los dos anteriores: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…

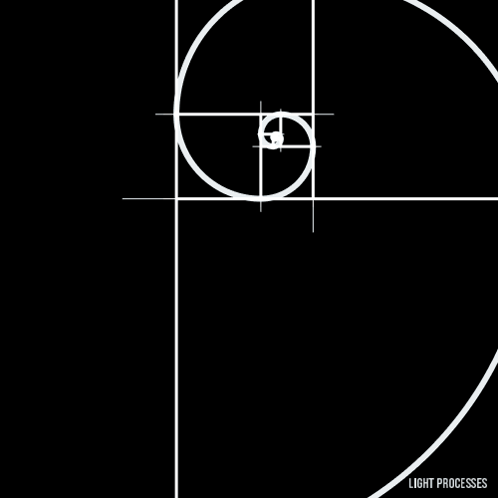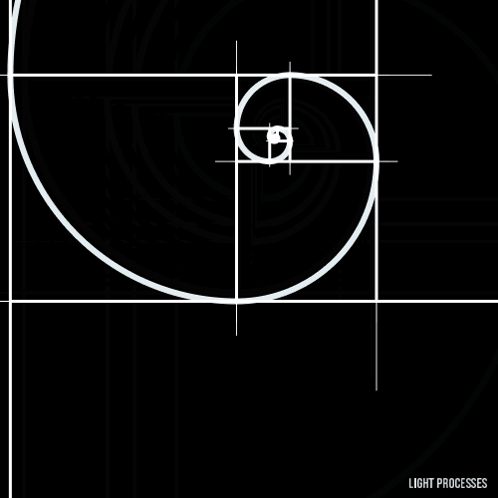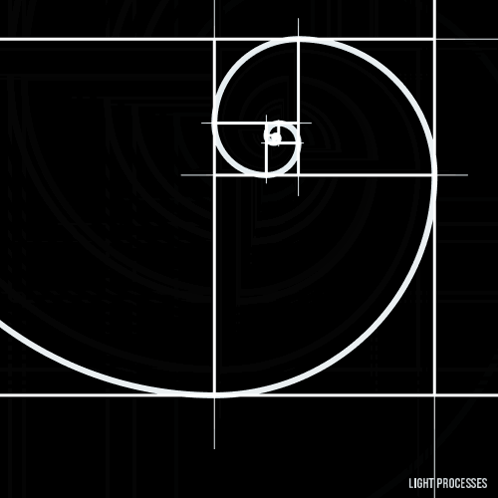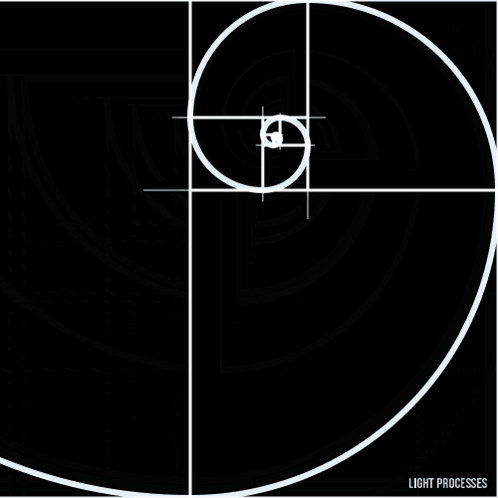
¿Por qué aparecen en espirales naturales? Aquí está la magia:

Cuando dibujas cuadrados con lados que miden números de Fibonacci consecutivos y trazas una curva que conecta las esquinas, obtienes una espiral logarítmica perfecta. Esta misma espiral aparece en:

• Caracoles: La concha del nautilus crece siguiendo esta espiral
• Girasoles: Las semillas se organizan en espirales que siguen números de Fibonacci (típicamente 21 y 34, o 34 y 55 espirales en direcciones opuestas). ¿Por qué? Porque esta disposición maximiza el empaquetamiento: caben más semillas en el menor espacio posible
• Piñas y piñas de pino: Los patrones en espiral de las escamas siguen números de Fibonacci
• Galaxias: Los brazos espirales de galaxias como la Vía Láctea siguen esta proporción
• Huracanes y sistemas climáticos: La estructura en espiral sigue patrones logarítmicos similares

¿Por qué la naturaleza «prefiere» estos números? Porque representan la forma más eficiente de empaquetar elementos en el espacio, maximizando la exposición a la luz solar (en plantas) o minimizando los espacios vacíos.

A medida que avanzas en la secuencia de Fibonacci, la razón entre dos números consecutivos se acerca cada vez más a phi (la proporción áurea). Por ejemplo: 89/55 ≈ 1.618.

Lo que nos lleva al siguiente número =

π (Pi) ≈ 3.14159…

¿Qué es? La relación entre la circunferencia de un círculo y su diámetro. No importa qué tan grande o pequeño sea el círculo, esta razón siempre es π.

¿Por qué es importante?

• Geometría y trigonometría: Fundamental para calcular áreas, volúmenes, ondas y movimientos circulares
• Física: Aparece en la relatividad general de Einstein, la mecánica cuántica, y la teoría de ondas
• Probabilidad: Sorprendentemente, π aparece en problemas de probabilidad (como la aguja de Buffon)
• Ingeniería: Esencial para diseñar cualquier cosa que gire: ruedas, engranajes, turbinas
• Procesamiento de señales: Las transformadas de Fourier (base de MP3, JPEG, radar) usan π extensivamente

Es uno de los números más computados de la historia: se han calculado más de 100 billones de dígitos.

e (número de Euler) ≈ 2.71828…

¿Qué es? La base de los logaritmos naturales. Se define como el límite de (1 + 1/n)ⁿ cuando n tiende a infinito.

¿Por qué es el número más importante del cálculo?

• Crecimiento exponencial: Describe crecimiento continuo en el tiempo. Si algo crece de forma continua (poblaciones, inversiones con interés compuesto, reacciones químicas), ahí está e
• Física: Aparece en decaimiento radiactivo, circuitos eléctricos, amortiguamiento de oscilaciones
• Biología: Modelos de crecimiento poblacional, propagación de epidemias
• Probabilidad: La distribución normal (curva de campana) incluye e en su fórmula
• Matemáticas: Es la única función f(x) = eˣ cuya derivada es ella misma. Esto la hace única y fundamental en ecuaciones diferenciales

Ejemplo concreto: Si inviertes $1 a 100% de interés anual compuesto continuamente, después de 1 año tendrás $e ≈ $2.72.

i — La unidad imaginaria: √(-1)

Qué es? Un número que, cuando lo elevas al cuadrado, da -1. Matemáticamente «imposible» en números reales, pero absolutamente real en sus aplicaciones.

¿Por qué es importante?

• Electricidad: Los circuitos de corriente alterna se analizan usando números complejos (a + bi)
• Mecánica cuántica: La ecuación de Schrödinger (base de toda la física cuántica) usa números imaginarios
• Procesamiento de señales: Las ondas se representan más fácilmente con números complejos
• Aerodinámica: El flujo de aire alrededor de alas se modela con funciones complejas
• Control de sistemas: Ingeniería de control (robots, drones, estabilidad) usa el plano complejo

Sin i,no tendríamos smartphones, computadoras cuánticas, ni la mayoría de la tecnología moderna.

✨ La identidad de Euler: e^(iπ) + 1 = 0

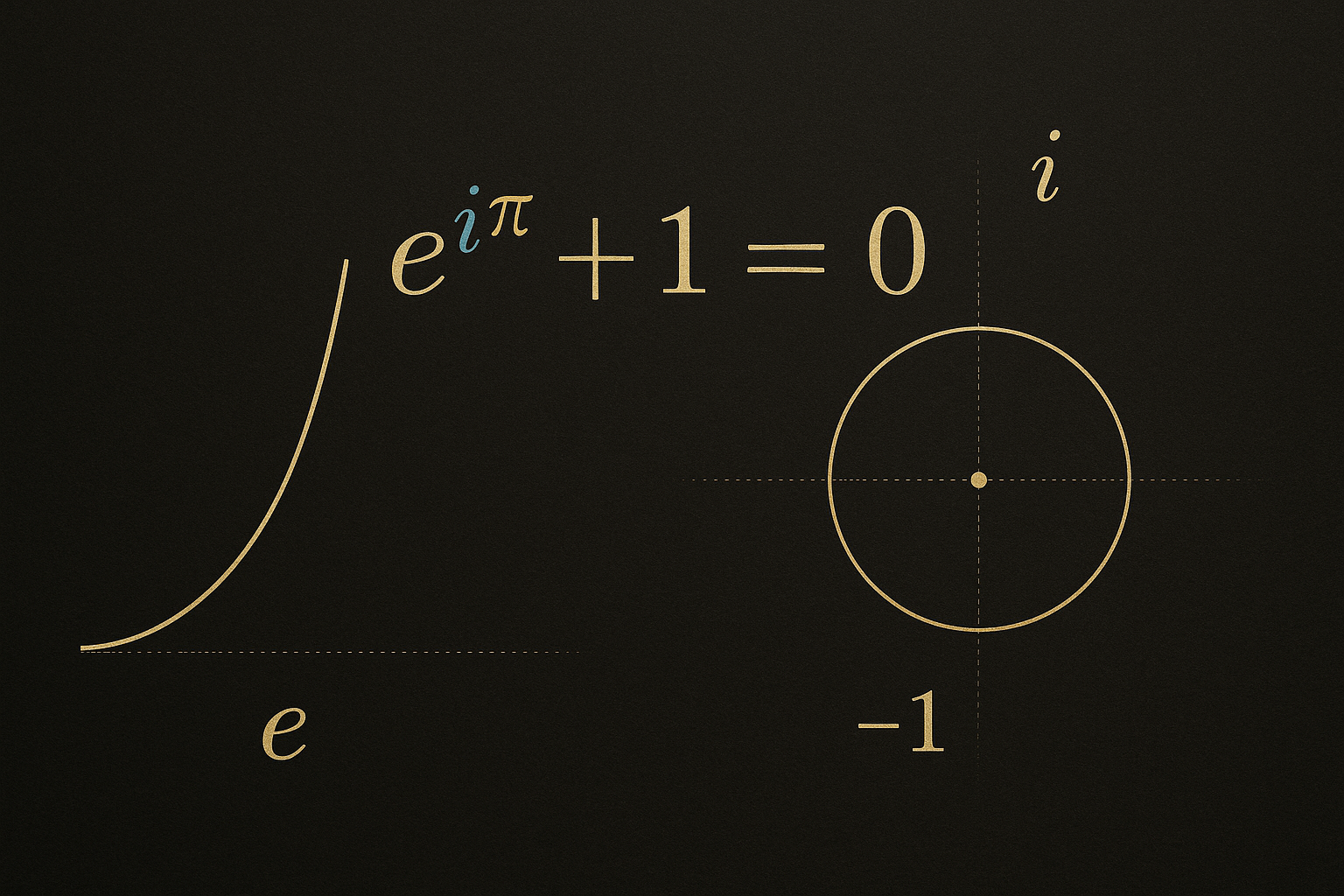
¿Por qué es «la ecuación más bella»? Porque conecta los cinco números más importantes de las matemáticas en una sola ecuación elegante:

• e (crecimiento)
• i (números imaginarios)
• π (geometría)
• 1 (unidad multiplicativa)
• 0 (unidad aditiva)

El matemático Benjamin Peirce dijo después de demostrarla: «Es absolutamente paradójica; no podemos entenderla, y no sabemos qué significa, pero la hemos probado, y por lo tanto sabemos que debe ser verdad».

🔢 Otros números extraordinarios

γ (Constante de Euler-Mascheroni) ≈ 0.5772…

Aparece en teoría de números, especialmente en problemas relacionados con números primos y la función zeta de Riemann. Aún no sabemos si es racional o irracional.

El número de Ramanujan: 1729

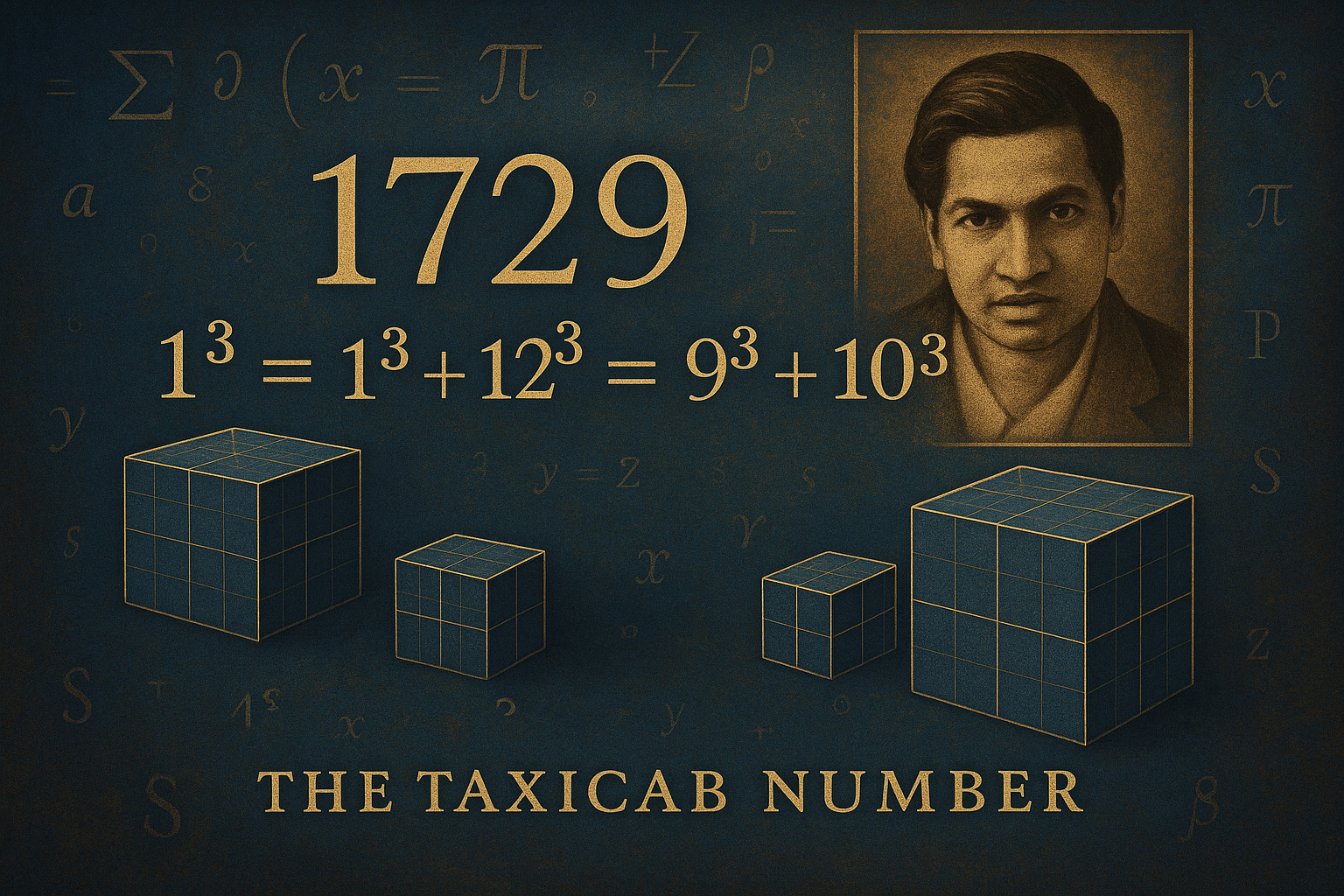
El matemático Srinivasa Ramanujan lo llamó «un número muy interesante». Es el número más pequeño que se puede expresar como la suma de dos cubos de dos formas diferentes:

• 1729 = 1³ + 12³ = 9³ + 10³

Estos «números taxicab» tienen aplicaciones en teoría de números y criptografía.

Número de Graham

Tan incomprensiblemente grande que si intentaras memorizar todos sus dígitos, la información no cabría en tu cerebro(literalmente: habría más dígitos que átomos en tu cuerpo). Se usó en un problema de teoría de grafos y es el número más grande jamás usado en una demostración matemática seria.

Números de Catalan

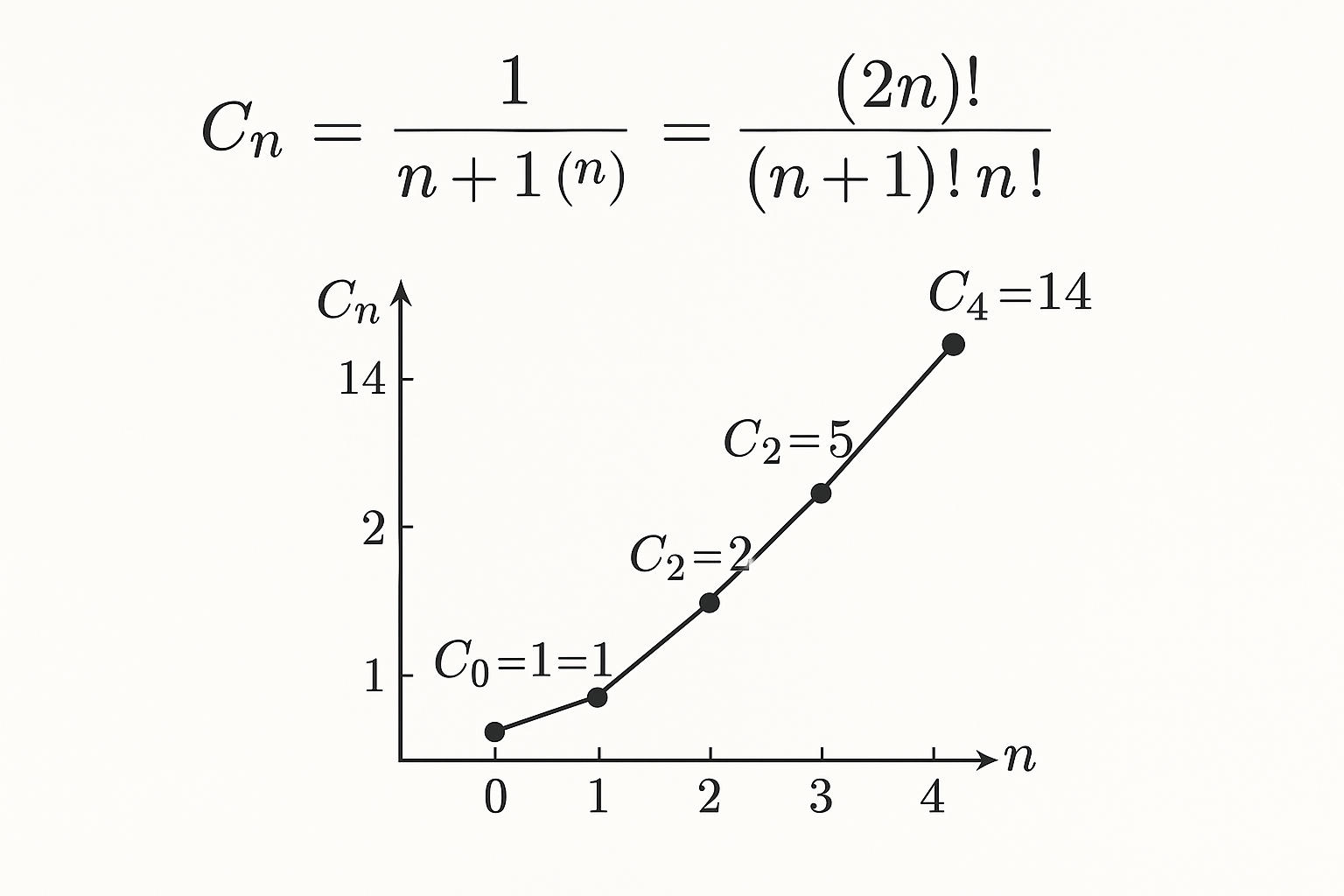
Cuentan formas de dividir polígonos en triángulos, formas de emparejar paréntesis, caminos en una cuadrícula sin cruzar la diagonal. Aplicaciones en ciencias de la computación y combinatoria.

🤔 ¿Por qué estos números importan?

No son solo curiosidades matemáticas. Son patrones fundamentales del universo:

• La naturaleza usa Fibonacci y phi para optimizar el crecimiento
• La física usa e, i y π para describir ondas, energía y espacio-tiempo
• La tecnología usa todos estos números para construir el mundo digital

Cada vez que escuchas música digital, usas GPS, tomas una foto, o envías un mensaje encriptado, estos números están trabajando silenciosamente detrás de escenas.

Las matemáticas no son solo números en un papel. Son el lenguaje secreto con el que está escrito el universo.

Referencias

• Livio, M. (2002). The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number. Broadway Books.
• Maor, E. (1994). e: The Story of a Number. Princeton University Press.
• Posamentier, A. S., & Lehmann, I. (2007). The Fabulous Fibonacci Numbers. Prometheus Books.
• Nahin, P. J. (1998). An Imaginary Tale: The Story of √-1. Princeton University Press.
• Stewart, I. (2017). In Pursuit of the Unknown: 17 Equations That Changed the World. Basic Books.
• Douady, S., & Couder, Y. (1992). «Phyllotaxis as a Dynamical Self Organizing Process.» Journal of Theoretical Biology, 178(3), 255-274.